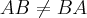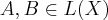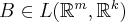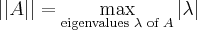Lecture 9
Review of linear transformations and matrices
We shall deal with maps 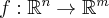 (from one Euclidean space to another), and try to understand what the derivative of such a map is.
(from one Euclidean space to another), and try to understand what the derivative of such a map is.
Here are some notions from linear algebra which will be used here.
- vectors and vector space
- linear combination of vectors and span
- linearly (in)depencce and basis
- dimension of a vector space, in particular, dim
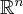 is
is 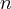
- linear transformation
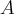 from a vector space
from a vector space 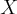 to another
to another 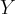 .
. 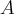 is called a linear operator if
is called a linear operator if 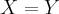 .
. - injective, surjective and bijective linear operator and inverse
- set of all linear transformations from
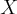 to
to 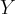 :
: 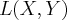 or
or 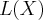 if
if 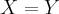
- Composition (product) of two linear transformations
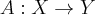 and
and 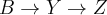 is
is 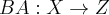 .
.
Theorem. A linear operator 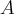 on a finite dimensional vector space is one-to-one if and only if the range of
on a finite dimensional vector space is one-to-one if and only if the range of 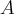 is all of
is all of 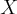 .
.
Theorem. Assume that the invertible linear operator 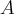 of
of 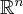 satisfies the inequality
satisfies the inequality 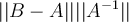 , for
, for 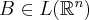 . Then
. Then 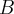 is invertible.
is invertible.
Theorem. Assume 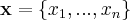 and
and 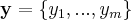 are bases of vector space
are bases of vector space  and
and  , respectively. Then every
, respectively. Then every 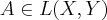 can be represented by a matrix
can be represented by a matrix ![[A] [A]](https://kurser.math.su.se/filter/tex/pix.php/7e2bf8880d46cb84f91d8740b2659a88.png) in the sense that
in the sense that ![[Y]_{\mathbf y}=[A][X]_{\mathbf x} [Y]_{\mathbf y}=[A][X]_{\mathbf x}](https://kurser.math.su.se/filter/tex/pix.php/7aa06793e0c522dc65315cc7c23b8fb9.png) .
.
Here is perhaps a new notion: Norm of 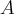 :
:  .
.
Theorem. The norm of 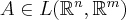 is finite and unifromly continuous, and for
is finite and unifromly continuous, and for
||A+B||\le ||A||+||B||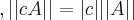 for scalar
for scalar  ,
, 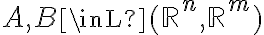 ;
;
With  defined as distance function
defined as distance function 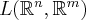 is a metric space. ◊
is a metric space. ◊
By Cauchy-Schwarz inequality, 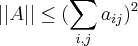 .
.
Proposition. If  is a metric space,
is a metric space, 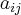 (
(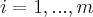 ,
,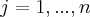 ) are real continuous functions on
) are real continuous functions on 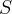 , and if for each
, and if for each 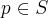 ,
, 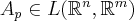 with matrix
with matrix 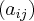 , then the mapping
, then the mapping 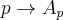 is a continuous mapping of
is a continuous mapping of 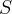 into
into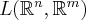 .
.
How to compute the norm of 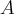 ? For example what is
? For example what is 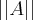 if
if 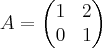 ? From the above inequality we get an upper bound for the norm:
? From the above inequality we get an upper bound for the norm: 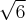 . Here is a computational formula for a norm of square matrix.
. Here is a computational formula for a norm of square matrix.
Theorem. (Peano) If 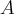 is an
is an 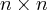 symmetric matrix, then all eigenvalues are real and
symmetric matrix, then all eigenvalues are real and
For any square matrix 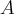 the eigenvalues of
the eigenvalues of 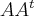 are all nonnegative definite, so
are all nonnegative definite, so 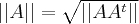 is the square root of the largest eigenvalue of
is the square root of the largest eigenvalue of 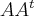 .
.
Using this theorem we can compute the norm of above matrix. 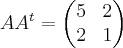 . The largest eigenvalue of this matrix is
. The largest eigenvalue of this matrix is 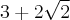 and hence
and hence 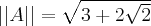 , which is below
, which is below 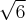 .
.