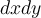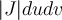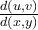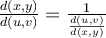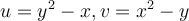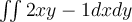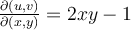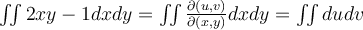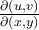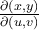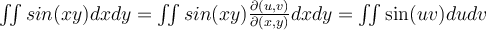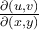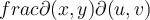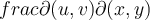Diskussionsforum

jacobianen

jacobianen

av Elie Sassine -
Antal svar: 8

Hej!

I boken och i de inspelade filmerna så har det stått att man gör del x , y med avseende på u , v om man ska göra en variabelsubstitution från x , y till u , v men i lösningen till dem rekommenderade uppgifterna (B8) står det del u , v med avseende på x , y.
Så jag undrar över vilken ordning man ska följa? jag vet att just i denna uppgift (B8) spelar det ingen roll för oavsett ordningen får man 1, var det ett sammanträffande? och finns det något specifikt jag behöver tänka på?

Tack!

Som svar till Elie Sassine

Sv: jacobianen

av Anders Mogren -

Du vill ha så att du kan ersätta dxdy med |J| dudv. Ibland kan det vara enklare att räkna ut \frac{d(u,v)}{d(x,y)}. Då kan du derivera i den ordningen och använda att \frac{d(x,y)}{d(u,v)}=\frac{1}{\frac{d(u,v)}{d(x,y)}}.

/A

Som svar till Elie Sassine

Sv: jacobianen

av Ludvig Olsson -
Precis som Anders skriver, beror det på vad som är enklast att räkna ut.

Om du har ett variabelbyte u=y^2-x, v=x^2-y och vill integrera över \iint 2xy-1 dxdy, är det lättare att märka att \frac{\partial(u,v)}{\partial(x,y)}=2xy-1 och att sedan använda att
\iint 2xy-1 dxdy=\iint \frac{\partial(u,v)}{\partial(x,y)}dxdy=\iint dudv (här har jag skippat absolutbelopp för tydlighet).

Man skulle också kunna försöka skriva u,v i termer av x,y, men det lär blir en ganska jobbig uträkning i det här fallet.

Det är inte alltid man har turen att hitta \frac{\partial(u,v)}{\partial(x,y)} i uttrycket man vill integrera, så då får man räkna ut \frac{\partial(x,y)}{\partial(u,v)} istället och lägga in den i integralen efter variabelbytet.
Som svar till Ludvig Olsson

Sv: jacobianen

av Elie Sassine -
Hej igen!
Det ni skrev hade jag förstått men min fråga var i både boken och de inspelade filmerna så står det \frac{\partial(x,y)}{\partial(u,v)} när man byter från x, y till u, v. Däremot så står det \frac{\partial(u,v)}{\partial(x,y)} i lösningsförslaget till B8. Varför? varför inte \frac{\partial(x,y)}{\partial(u,v)}?
Som svar till Elie Sassine

Sv: jacobianen

av Ludvig Olsson -
Hej.

I B8 är Jacobianen 1, så båda metoder fungerar på samma gång. Vi har att

\iint sin(xy)dxdy=\iint sin(xy) \frac{\partial(u,v)}{\partial(x,y)} dxdy=\iint \sin(uv) dudv.

Du skulle lika gärna kunnat räkna ut Jacobianen i andra ordningen.
Som svar till Ludvig Olsson

Sv: jacobianen

av Elie Sassine -
ja, det hade jag också skrivit i mitt första inlägg, så min fråga är igen "är detta ett sammanträffande? alltså har man skrivit \frac{\partial(u,v)}{\partial(x,y)} av någon specifik anledning? för vanligtvis och i alla andra uppgifter har man skrivit \frac{\partial(x,y)}{\partial(u,v)} när man vill gå över från x, y till u, v.
Om min ovanstående fråga är otydlig: är det rent matematiskt korrekt att skriva frac{\partial(x,y)}{\partial(u,v)} då man ville gå över från x, y till u, v i B8? (Obs jag vet att i just detta fall så skulle det inte spela någon roll för frac{\partial(x,y)}{\partial(u,v)} och \frac{\partial(u,v)}{\partial(x,y)} skulle leda till samma svar.)
Som svar till Elie Sassine

Sv: jacobianen

av Ludvig Olsson -

Hej. Det är helt ett sammanträffande att det står \frac{\partial(u,v)}{\partial(x,y)} i den här lösningen.

Som du skriver spelar det inte någon roll i det här fallet, och därmed är det matematiskt korrekt att skriva i båda ordningar i det här fallet. 

Jag tror inte att jag exakt förstår din fråga, att något är matematiskt korrekt innebär väl bara att du har kommit fram till lösningen på något sätt?

Som svar till Ludvig Olsson

Sv: jacobianen

av Elie Sassine -
Okej, hade det inte varit ett sammanträffande, alltså hade del u, v / del x, y lett till ett svar och del x, y / del u, v lett till ett annat svar och både var lika enkla att räkna. Skulle vi ha skrivit del u, v/ del x, y eller del x, y /del u, v för att gå över från x, y till u, v?
Som svar till Elie Sassine

Sv: jacobianen

av Ludvig Olsson -
Det beror på problemet lite, oftast skriver vi frac{\partial(x,y)}{\partial(u,v)} om vi vill gå över från x,y till u,v och då lägger vi in jacobianen i vår nya integral.

Ibland kan vi hitta inversen till jacobianen i vår första integral, och kan vi istället räkna ut frac{\partial(u,v)}{\partial(x,y)}. Mitt första svar har ett exempel på det.