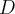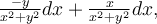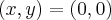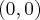Hej.
Om det är tillåtet att använda Greens sats beror inte bara på området, utan även formen/vektorfältet man integrerar över. Den måste vara definierad inuti det område
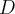
som dyker upp i Greens sats. I exemplet integreras det över formen
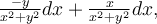
som inte är definierad i punkten
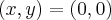
. Faktum är att den är definierad överallt annars, så punkten
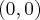
är en sorts singularitet till funktionen, vilket bidrar till att integralen inte är 0.
Lösningsförslaget i uppgiften skulle kunna vara tydligare, det går att definiera matematiskt vad det innebär att deformera enhetscirkeln men det är inte särskilt lätt och inte något ni har gått igenom.
Tänk istället så här: Om du ritar enhetcirkeln tillsammans med (den inre) kurvan i uppgiften på planet, får du en figur som ser (ungefär) som två cirklar kring origo som skär varandra i en punkt. Om du nu tittar på området mellan de två cirklarna kan du använda greens sats, eftersom formen ovan är definierad i området.
Randen till området går först genom den yttre cirkeln (motsols) och sedan genom den inre cirkeln (medsols). Enligt Greens sats är hela integralen 0, så integralen över den yttre cirkeln (motsols) + integralen över den inre cirkeln (medsols) är 0. Men integralen över den inre cirkeln (medsols) är - integralen över den inre cirkeln (motsols). Alltså är
Integral över yttre cirkeln (motsols)= Integral över inre cirkeln (motsols).
Den inre cirkeln är enhetscirkeln. Du kan ofta resonera på samma sätt med andra typer av kurvor. Det är svårt att skriva ned sådana här lösningar med ord, så om du är förvirrad av något kan du skriva det så ska jag försöka ge en förklaring.
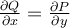 och kurvintegralen är
över ett område för vilket vi kan använda Greens, så blir kurvintegralen
0. Men sen visar han på enhetscirkeln att integralen inte blir 0.
Varför kan vi inte använda Greens formel över enhetscirkeln?
och kurvintegralen är
över ett område för vilket vi kan använda Greens, så blir kurvintegralen
0. Men sen visar han på enhetscirkeln att integralen inte blir 0.
Varför kan vi inte använda Greens formel över enhetscirkeln?