As title suggests I am having a hard time understanding the proof for TH.6.15. I looked up an explanation online, but I still don't seem to get it.
Attached is a photo of a part of an answer i found that i don't quite get: 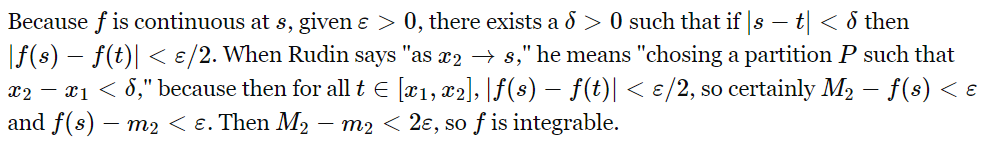
How are we sure that $M_2 - f(s) < \varepsilon$? We know that $M_2 = sup_{[s, x_2]}(f(x))$, and I'm thinking that this (even though it is bounded) could make $M_2 - f(s)$ greater than $\varepsilon$.
I know my thinking is off, but I don't know where. Thanks in advance!