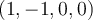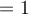Hello, I have a question about question 5. Perhaps it's just something I've missed so far, but doesn't the implicit function theorem require that the equations defining the hypersurface are zero on the point we apply it to? As far as I can see, neither the function xu + y^2v nor the function xv^4-y^3u^5 are zero at (x=1, y=-1, u=0, v=1)? Or are the equations given meant to be transformed somehow?
Thanks,
Sofie