If someone took notes today, I'd be happy if you could send them (I could not attend).
Best,
Ben
I uploaded my corrected notes. We did not go over fg+alg implies finite (last page and half)
I added the proof of finite implies finitely generated that was missing (the clever one, not the super long one I created on the spot when I realized I had a gap in my notes) I corrected the the part about iso of simple extensions: we have to require that alpha goes in beta in order to get the same minimal poly. I give an example showeing that this hast to be the case.
MVH
Sofia
P.S>. do not get used to me uploading notes. I will do it just if I feel they are tidy enough :)
It seems like you want to say that assuming that α is algebraic then p(α) for some non-zero p(x) in F[x], but then ker eval_α neq 0, so eval_α not injective.
Best,
Ben
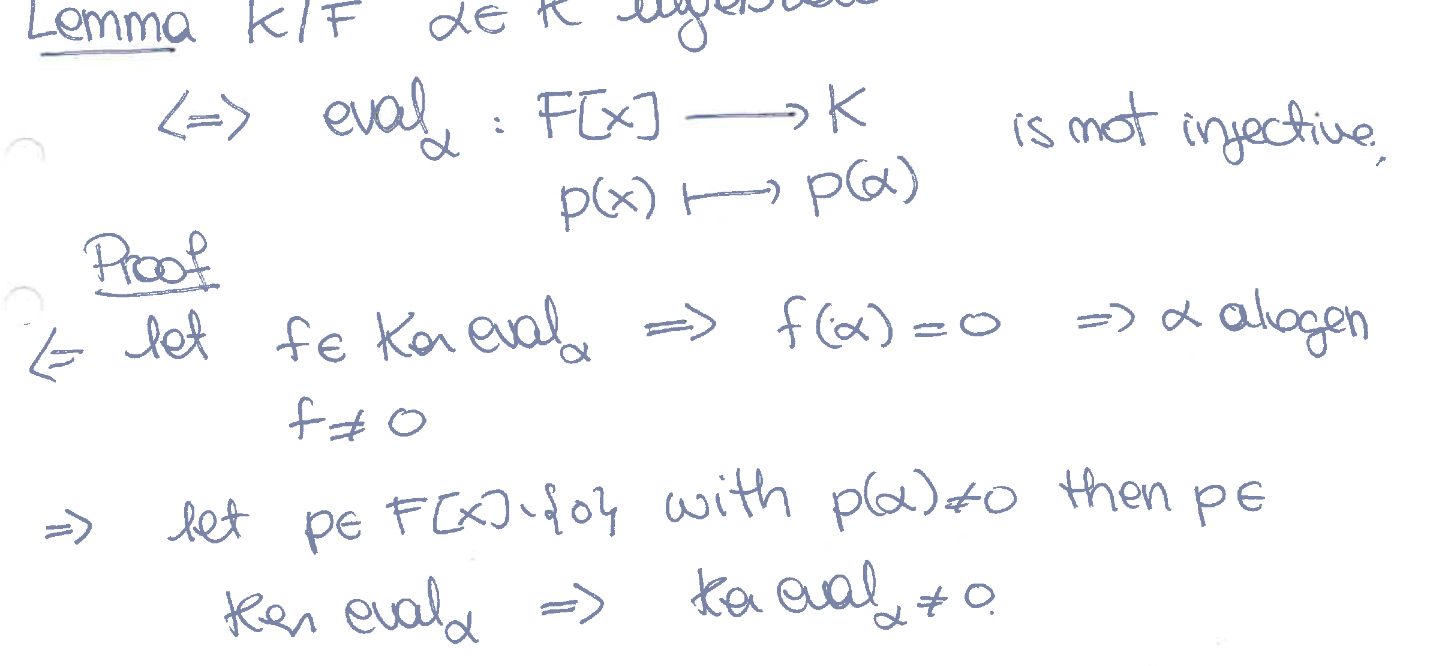
Yes the two arrows are in the wrong direction. You can also prove the two directions at once eval not injective iff there is a non trivial element p in the kernel, if there is a non zero poly p that vanishes if evaluated at alpha.
Yes! You are right. In adfition the two arrows are in the wrong direction.
You can also prove the two directions at once eval not injective iff there is a non trivial element p in the kernel, if there is a non zero poly p that vanishes if evaluated at alpha.. so this not really a bug deal.
This is exactly the reason I do not usually make my notes public: for a proof like that that I could do I woken up in the middle of the night, I write them down just to estimate the time I will need to present them (I know 2x45 minutes leq 4 pages of notes) without taking care of them being perfect/correct (as you are starting of discovering with my swapping of Fs and KS I do not always write what my brain means) :)