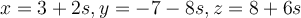Tryckfelswiki

FEL I TEXT

Kap 2: På sidan 43, i beräkningen av determinanten i exemplet högre upp på sidan står, i näst sista ledet, termen 5(28+12). Talet 12 i parentesen är fel! (RÄTT: 10, ty 5*(-2)=-10) Rätt värde på determinanten av 3x3-matrisen är 198.

Kap 2: På sidan 50, exempel 2.1, andra raden i kalkylen: Elementet 4 på rad 2 kolonn 5 skall vara -4. Man kan "fixa" problemet genom att byta ut -7 i startdeterminanten mot 1, så stämmer beräkningarna.

Kap 4: I Sats 4.3 har ett villkor trillat bort, nämligen att antalet ekvationer ska vara exakt lika många som antalet obekanta (alternativt kan detta formuleras som att koefficientmatrisen ska vara kvadratisk)

Kap 5: På sidan 123, sista raden, är associativa lagen fel. Skall vara som i övning 1 på nästa sida.

Kap 5: På sidan 125, definitionen av skalär*vektor, saknas fallet lambda=0.

Kap 5: På sidan 137, Sats 5.4, saknas förutsättningen att vektorerna ej är nollvektorer.

Kap 6: På sidan 153, mitten: Stryk parentesen "(Om vi väljer   ...   förstås...)".

Kap 7: Exempel 7.1;För s=-1 fås inte P iför den andra parametriseringen av linjen .

Enklaste sättet att få texten att fungera som den var avsedd att göra är att ändra den andra parametriseringen till

.

Om man då sätter 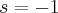  får man .

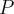 Exempel 7.18 Det ska vara 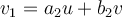$v_1 = a_2u+b_2v$ istället för $u_2 = a_2u+b_2v$.

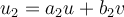Kap 9: S 310, formeln för kvadratkomplettering ska vara 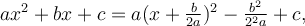$ax^2+bx+c=a(x+\frac{b}{2a})^2-\frac{b^2}{2^2a}+c,$.

UPPGIFTER: FEL I FACIT

Kap. 1:

  8. I matrisen A-B+C är elementet 6 fel (RÄTT: 8), och -A+2(3B-C) är 16 fel (RÄTT 31)
  9. I matrisen X är 4/3 fel (RÄTT: -8/3)
10. I matrisen AA är 6 fel (RÄTT 12), och i AB är hela första raden:  -11 -13 5  fel (RÄTT: -31 37 -5), och i BD är 13 fel (RÄTT 15), och i DD är 13 fel (RÄTT 23).
11. A är fel: (det ska vara y=-1/t istället för 1/t).

14a Faktoriseringen av A+AB saknas, den är A(E+B).

22b. Faktoriseringen skall vara (2A-3B)(2A+3B)

Kap 2:

12. Uppgiften, och lösningsförslaget, använder senare teori (Sats 4.7). Om man formulerar om uppgiften till att fråga efter vilka d som matrisen har determinant 0 går den dock att lösa med kapitlets metoder.

16.  Det ska vara  det((1/3)A)=(1/3)^3 det(A)  eftersom A är en 3x3 matris.

Kap 3:

8. I lösningen till andra ekvationssystemet skall det vara x1 = 4/17 + s/17.

10. Två delamedstecken har fallit bort.

12. Lösningsförslaget använder senare teori (Sats 4.7). Uppgiften går dock utmärkt att lösa med kapitlets metoder. (Den som läser lösningsförslaget noterar dock ett tryckfel: determinanten skall vara a^2(a-1))

15. Fel i uppgiften: Matriselementet 12 i andra termen skall vara 2.

Kap 4:

4. Beskrivningen av AA_3 är fel, det skall vara "Från den andra kolonnen subtraheras 2 gånger den sista kolonnen".

5. Översta raden på matrisen i lösningen är fel och ska vara 1  a  1  0. Dessutom är det i fallet a^2-5=0, men b inte 0, som lösningar saknas.

7. Lösningen x skall vara x = (de-bf)/(ad-bc)

14. Determinanten av koefficientmatrisen ska vara 2(a^2-5). Detta påverkar emellertid inte svaret.

15. x_3 bör vara 1-10 = -9 respektive b_1 - b_2.

Kap 5:

11. Rätt svar är 6, inte 12 (vinkeln mellan AB och BC är 120 grader eftersom vinkeln mellan BA och BC är 60 grader).

23.  v1 = e1 + (1-sqrt(2))*e2,      v2 = -sqrt(2)*e1 + 2*e2,      v3 = (1+sqrt(2))*(e2-e1)

Kap 6:

2. Fel i uppgiftsformuleringen: "också är linjärt oberoende" skall vara "är linjärt beroende".

17b. Determinanten är 0, inte 3.

24c. Nedre högra elementet i matrisen B skall vara 5/4.
    d. Koordinatvektorn efter "Därmed" skall vara kolonnvektorn med element 3,1,2, inte den 3x3 matris som står där.

Kap 7:

4. Fel i uppgiften: I parametriseringen av l2 skall det vara x = 1+s.

20. Fel i uppgiften: Parameterlinjen skall vara  x = 1-3t,   y = 2+t.

Kap 9:

9. Svaret som står i facit är fel, efter det att rotationen som eliminerar den blandade termen och en korrekt lösning ger att ekvationen för kurvan blir

2(X-3/Sqrt[2])^2+4(Y+1/Sqrt[2])^2=3,

i de roterade koordinater som är angivna i facit, d v s x=(X-Y)/Sqrt[2] och y=(X+Y)/Sqrt[2]. Löser man dessa för X och Y får man

X=(x+y)/Sqrt[2] och Y=(y-x)/Sqrt[2] (OBS! står fel uttryck för Y i facit!)

För att se detta, lite mer räknemässigt lättare än att bara räkna på, byt koordinater till S, T så att

x= S-T och y=S+T. (Vilket svarar mot att S=X/Sqrt[2] och T=Y/Sqrt[2].)

Det ger att ekvationen i (S,T) koordinater blir 8 - 12 S + 4 S^2 + 8 T + 8 T^2, eller efter kvadratkomplettering

4(S-3/2)^2+8(T+1/2)^2=3.

Sätt sedan in S=X/Sqrt[2] och T=Y/Sqrt[2], och skriv om, så fås resulatetet ovan. Kurvan är alltså (i alla fall) en ellips.

12. För lambda=0 fås inte en dubbellinje utan två parallella linjer: x=0 resp. x=2.