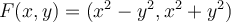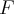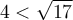Hej!
Jag har hamnat lite på efterkälken men ska försöka hinna med så mycket som möjligt. Jag fastnade med integralen 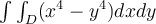 över området
över området 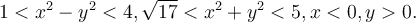
Jag gjorde variabelbytet 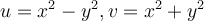 och fick nya integralen
och fick nya integralen 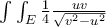 efter att jag räknat ut jakobianen och bytt variabler.
efter att jag räknat ut jakobianen och bytt variabler.
Vad jag har svårt att förstå är hur det här ger mig integralen över området i endast en kvadrant, vilket verkar vara fallet eftersom jag får rätt svar utan att dela resultatet med 4. Jag undrar också om det spelar någon roll här att jag ska integrera över just den andra kvadranten, blir inte resultatet precis detsamma oavsett vilka tecken jag har på x och y?
Allt gott
Petrus