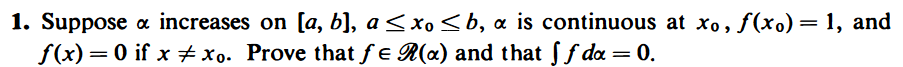

I understand why the function is not Riemann-integrable but is R-S integrable, since the upper and lower sum wont equal eachother since when the partition "encounters" x_0 we get that sup f(x) will be 1, meaning that one delta x_i will be present for U(P,f), but not L(P,f) since we would always choose an x that makes f(x) = 0 in L(P,f):s case. So it isnt Riemann-integrable. I also understand the proof for showing how if we can bound it with an epsilon, then we can know that it is R-S integrable. What I dont understand is how we can be sure that the specific integral value will be 0.