Ämnesdisposition
-
- Instructor: Sofia Tirabassi tirabassi@math.su.se
- TA: Jan Mcgarry Furriol jan.mcgarry.furriol@math.su.se
- Office Hours: Please contact me by email to discuss your questions or to schedule a meeting.
- Textbook: Abstract Algebra by Dummit and Foote.
Time and Place
- Lecture hours hours: Mondays and Thursdays 13-15
- Review session
: Mondays and Thursdays 15-16 starting from the second lecture.
- Important: The review sessions are an integral part of the course, and it is crucial that you attend them. Some important examples will be introduced during the review sessions, and relied on in subsequent lectures. All problems and examples that are done during the review sessions are considered fair game for the final exam.
- Lectures will be conducted on campus
Examination
- The grading scheme for the course will comprises three parts: (1) Final written exam, (2) Final oral exam and (3) homework.
- Recommended practice problems will be posted, and some of them will be solved during the review sessions.
- The final written exam will be worth 24 points. Deonte by
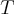the score received. - You need to score 15 points or higher on the final exam to pass (So
).
- You can raise your grade by up to 3 extra credit points by successfully completing the homework assignments. For example, if you get 11 on the exam and 2 on the homework, your overall score for the exam is 13 and you pass.
- Examination Rules at the Department of Mathematics.
- Everyone who has taken 21 or more points in the written examination (+ bonus) can access to the oral examination.
- The oral examination is worth 3 points. Denote by
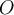the oral score. Your final exam score will be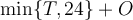 
- Grading scale: 27+= A, 24-26.9= B, 21-23.9= C, 18-20.9= D, 15-17.9=E, 15-=F
Homework Assignments
There will be 3 homework assignments in total . Homework counts towards 3 extra credit points. Theoretically you can receive a perfect score without doing any homework, but you are Strongly Encouraged to do all the homework.
Important announcement regarding exam registration.
Please keep in mind that exam registration closes 8 days before the exam date and that the university can not accept late registrations. If you have failed to register, you must write the re-examination.
Here are the instructions how to view your exam room. You must register via Ladok.
Go to https://schema.su.se and log in with your SU account.
1. Find your upcoming exam and click on the schedule for the exam. If there are multiple rows (i.e., multiple booked halls) for the same exam, click on any row.
2. A box will open - click on the link "Tentamensplacering: exam.timeedit.com". A new website with the exam details opens.
Under "Ditt schema" / "Your schedule", write in your 12-digit social security number on the exact form YYYYMMDD-XXXX (note 4 digits in the year and hyphens before the last 4 digits) in the box for "Student id", and then click on the green "See schedule" button. Now you should be able to see that room and your exact location!
-
The course covers the basic theory of groups and rings.
Roughly the first two thirds of the semester will be spent on groups. We will start with examples of how groups arise naturally in different areas, often as groups of symmetries (automorphisms). Some examples: Permutation groups, General linear groups, subgroups of general linear groups arising from linear algebra, dihedral groups.
After introducing some examples, we begin to develop the theory. It is important to not just consider groups in isolation, but to study their relation to each other. For this purpose we introduce the concepts of homomorphism, isomorphism, kernel, normal subgroup, quotient group; the three isomorphism theorems.
One of the main motivations for inventing groups is that they provide a good framework for studying symmetries. The relationship between groups and symmetries is encoded in the concept of a group action. Group actions are the reason that groups play a central role in other branches of mathematics, and also outside of mathematics. But group actions are useful also for the study of groups themselves: one can learn a lot about the structure of groups by investigating the way they act on other objects. Important examples: Action of G on itself by left multiplication and by conjugation.
Using what we learned about group actions and the Isomorphism theorems, we will prove Sylow's theorems and some related results about groups whose order is a prime power. Sylow's theorems are the first deep results we encounter about the structure of finite groups. We can use them to classify groups of certain orders, and to show that there are no simple groups of certain orders. For example, we will check that a simple group of order at most 100 necessarily has order 60 (in fact it is isomorphic to the alternating group A_5).
The Sylow theorems are the culmination of our study of groups. After that, we will move on to the second part, which is concerned with rings. Here is the outline of the second part:
Basic definitions about rings and fields, including: Ideals, prime ideals, maximal ideals, integral domains.
Important Classes of Rings: Euclidean Domains, Principal Ideal Domains (PID), Unique Factorization Domains (UFD).
Important Classes of ideals: Maximal ideals, prime ideals, principal ideals, finitely generated ideals.
Important Classes of elements: Units, irreducible elements, prime elements, nilpotent elements and zero-divisors.
Examples of rings and their applications: Chinese Remainder Theorem, Polynomial Rings, irreducibility criteria.
-
Definition of a group. Elementary consequences of group axioms.
Basic examples: Cyclic, symmetric and dihedral groups.
Dummit & Foote, Sections 1.1-1.5
Recommended problems: Section 1.1 problems 6, 7, 9, 22, 25
Section 1.2 problems 7, 9, 10
Section 1.3 problems 1, 3, 11, 12
-
Group homomorphisms and group actions. Subgroups.
Dummit & Foote sections 1.6-2.1
Recommended exercises: Section 1.6 3, 4, 6, 14 (very important!), 18, 20
Section 1.7 1, 4, 10, 15, 16, 18
Section 2.1 1, 2, 6, 10,15
-
Centralizers and normalizers, stabilizers and kernels.
Dummit & Foote, Sections 2.2-2.4
Recommended exercises: Section 2.2 5, 10
Section 2.3 9, 11, 25
Section 2.4 6, 14, 16
-
Left and right cosets. Normal subgroups. Quotient groups. Lagrange's theorem.
Dummit & Foote sections 3.1-3.2
Recommended exercises: Section 3-1, exercises 1, 6, 7, 24, 30, 43(highly recommended)
Section 3-2, exercises 6, 8, 11
-
Quotient groups and isomorphism theorems.
Dummit & Foote 3.1, 3.3
Recommended exercises: Section 3.1 11, 14, 15, 16, 34, 41, 42
Section 3.2 18, 22
Section 3.3 3, 4 (boring but useful), 7, 10
-
Alternating groups. Group actions revisited. Cayley's theorem.
Sections 3.5, 4.1, 4.2 (start)
Recommended exercises: Section 3.5 3, 4, 16
Section 4.1 2, 4, 9, 10
Section 4.2 2
-
Proof of Sylow's theorems.
Dummit & Foote, Section 4.5.
Recommended exercises: Section 4.5 4, 9, 10, 16, 37
-
Classification of finite abelian groups
Dummit and Foote 5.1-5.2
Suggested exercises
5.1: 1, 2, 4, 10
5.2: 1-4
-
Introduction to rings: definition and basic examples. Ring homomorphisms and quotient rings.
Dummit & Foote sections 7.1-7.3
Recommended exercises: Section 7.1 5, 6, 7, 9, 15, 21
Section 7.2 2, 5, 7
Section 7.3 1, 2, 15, 16, 24, 26, 28, 33, 34
-
Properties of ideals, rings of fractions, the
Chinese remainder theorem.Dummit & Foote sections 7.4-7.6
Exercises: Section 7.4 9, 11, 14, 15, 19, 20, 30, 31, 32, 33
Section 7.6
-
Principal ideal domains.
Unique factorizaiton domains.
Dummit & Foote sections Dummit & Foote sections 8.2- 8.3, 9.2-9.4
Recommended exercises: The ones of section 9.4 are the most important!
Section 8.2 1, 2, 3, 8
Section 8.3 1, 5, 6, 7, 8
Section 9.2 1, 2, 3, 4, 5 Exercise 1, 2, and 3 wil be partially covered during the lectures next week, but it would be great if you can try to look at them so that the lecture will go more smoothly :)
Section 9.4: 1, 2. Attention, you will need to show that a given polynomial is irreducible to solve part of exam exercises.
-
Continuation of the proof of UFD implies R[X] UFD
Field extensions
Dummit & Foote, Sections 9.3 13.1 13.2
These Exercises will be important for the exam
Exercises 13.1 1, 2, 3,4,7
Exercises 13.2: 2, 3, 4, 5, 7, 10, 12
-
More on field extesnions
-
Hello everybody,
As announced during the lecture, I upload short notes on Gauss lemma and some examples. Please read over it, if there is something you do not understand or need more details, we can discuss it on Tuesday.
With best wishes and good luck,
Sanaz
-
-
Review for the final exam.