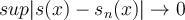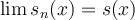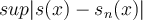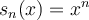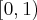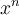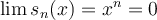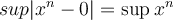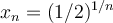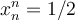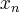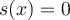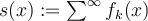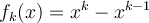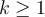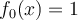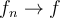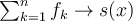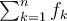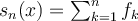Hej,
Jag har svårt att förstå funktionsserier. Jag förstår inte definitionerna för punktvis och likformig konvergens. I kompendiet står:
För 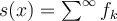 , och
, och 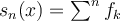 , så är
, så är 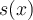 punktvis konvergent om
punktvis konvergent om 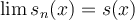 , och likformig konvergent om
, och likformig konvergent om 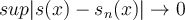 . Jag förstår inte vad skillnaden är. Om vi skiver om defintionen av punktvis konvergens så får vi:
. Jag förstår inte vad skillnaden är. Om vi skiver om defintionen av punktvis konvergens så får vi:
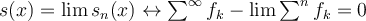 , men precis som i beviset till Weierstrass Majorantssats så är detta samma som
, men precis som i beviset till Weierstrass Majorantssats så är detta samma som 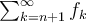 . Härifrån ser jag bara sättet som i Weirstrass bevis för att fortsätta, dvs hitta en konvegent följd
. Härifrån ser jag bara sättet som i Weirstrass bevis för att fortsätta, dvs hitta en konvegent följd 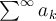 och skriva om
och skriva om 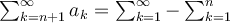 vilket måste gå mot noll då
vilket måste gå mot noll då 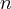 går mot oändligheten. Men då har vi bevisat likformig konvergens enligt Weierstrass. Så vad är skillnaden?
går mot oändligheten. Men då har vi bevisat likformig konvergens enligt Weierstrass. Så vad är skillnaden?
Jag är också förvirrad kring vad skillnaden är till vanliga definitionen av generaliserade serier? För funktionsföljder ville vi att 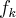 skulle konvergera till någon
skulle konvergera till någon 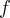 , här vill vi att
, här vill vi att 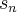 ska konvergera till
ska konvergera till 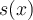 , men
, men 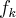 stannar samma? Men hur vet vi vad
stannar samma? Men hur vet vi vad 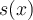 är? Definitionen av
är? Definitionen av 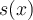 som en generaliserad integral är just gränsvärdet av
som en generaliserad integral är just gränsvärdet av 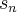 , eller missar jag något?
, eller missar jag något?
Tack!
Nestor