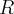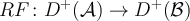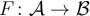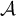Avsnittsöversikt

  • Fäll ihop Expandera

    Derived Categories VT26

    Fäll ihop allt Expandera allt

    Time: Thursdays 9:15–11:00 till March 26th, then 10:15–12:00 for the remainder of the semester.
    Place: Cramér room (SU Campus Albano, house 1, floor 3 — entrance near the Sonya Kovalevsky display)

    Exceptions to the schedule:

    • Thursday January 22nd 2026 the course will be 10:15–12:00 in Cramer.
    • Thursday February 5th we skip due to an interesting seminar at KTH.

    Teachers:

    Material: 

    • Gelfand–Manin, Methods of homological algebra (available for free from SU/KTH library website) [GM]
    • D. Huybrechts, Fourier–Mukai transforms in algebraic geometry [Huy]
    • A. Yekutieli, Derived Categories (free arXiv-version) [Yek]
    • Various scientific papers (more information below)

    Examination: Consists of two parts:

    1. Homework problems during the course (see below)
    2. A presentation (details announced during the course; 35 mins each, towards the end of the course, preliminary April 16–June 4)

    IMPORTANT: if you are a MASTER STUDENT and want to take the course for credit you have to have it registered as a selected topic in mathematics (write to Jennifer to do it). In addition, to the above 1 and 2 there will also be a short oral examination for you. If you don't want credits for the course, we could instead write a certificate that you have followed the course.

    About:  

    In the past three decades, triangulated categories in general and derived categories in particular have been useful tools in many areas of mathematics. In this course we are going to introduce triangulated categories but focus on the main example: the (bounded) derived category of an abelian category.
     
    The course is roughly divided in two parts. The first is purely algebraic, more or less covering
    • additive categories and functors
    • abelian categories and exact functors
    • axioms of triangulated categories
    • construction of the derived category of an abelian category
    • derived functors
    In the second part, we are going to present brief overviews of several applications, mainly to the field of algebraic geometry.
     
    Below (see modules) you will be able to find a more detailed lecture by lecture plan which will be constantly updated during the course.
     
    Prerequisites:  For the first part some basic homological algebra: the tensor product is required and preferably you have seen Tor and Ext. The latter are motivations for the general constructions that otherwise could be difficult to understand and motivate. For the second part some knowledge about sheaves and algebraic geometry will be beneficial, however this is not necessary to complete the course. In particular, most/all homework will be on the first part.


    Homework problems
    If you are taking the course for credit, you should solve the exercises and submit your solutions (on Moodle). If you cannot make it by the date indicated for some reason, that is probably fine – just write to us ahead of time to let us know. If you have discussed the problems with others (which we encourage you to do), please indicate this in your hand-in. Also, if you have used other sources (forums, Stacks project, AI, ...) please indicate this as well.

  • Fäll ihop Expandera

    Homework Assignments

    • Homework 1 Inlämningsuppgift
      Öppnades: måndag, 12 januari 2026, 00:00
      Senaste inlämningsdatum: torsdag, 5 februari 2026, 23:59
    • Homework 2 Inlämningsuppgift
      Öppnades: fredag, 27 februari 2026, 00:00
      Senaste inlämningsdatum: torsdag, 19 mars 2026, 23:59
  • Fäll ihop Expandera

    Presentation

    When you have chosen a project, please email David and Sofia and we will list them here.

  • Fäll ihop Expandera

    Lecture 1: Introduction and motivation

    After a brief introduction with motivations we will start to review a bit of category theory. We will introduce additive categories and functors and we will start to delve into abelian categories.

    Literature

    [Yek] We do as much as possible of chapter 2, we will continue into the next lecture.

    One can find some of the material in [GM] and [Huy] but treated much more superficially.

  • Fäll ihop Expandera

    Lecture 2: Abelian categories

    We keep going over [Yek] Chapter 2.

    Important notions

    • additive categories and functors
    • abelian categories
    • exactness properties for functors
    • projective and injective objects
    • there are enough of them in R-mod.
  • Fäll ihop Expandera

    Lecture 3: Abelian Categories and complexes

    We introduce (filtered) limit and colimits and overview the axioms ABxyz by Grothendieck. If you can read math French (that is if you speak fluently a romanic language) you can go directly at the source. Otherwise 

    The Stack Project

    is always a good source.

    For limits and colimits I used MacLane's book, but I am told Riehl's Category theory in context is a better choice.

    I also introduced the categories Kom(A) of complexes over an abelian category and the homotopy category. We have seen how a map of complexes induces a map in cohomology and how you can use diagram chasing in any abelian category.

  • Fäll ihop Expandera

    Lecture 4

    I showed that a morphism in an abelian category induces a morphism of projective resolutions which is unique up to homotopy equivalence. This is Gelfand–Manin III.1.3–1.4.

    Then we constructed mapping cones and distinguished triangles in the homotopy category. We showed that distinguished triangles satisfies the five axioms TR0–TR5. You can find this in Kashiwara–Schapira, Sheaves on Manifolds, I.1.4.

  • Fäll ihop Expandera

    Lecture 5 (Feb 19): Construction of the derived category

    We constructed the derived category. In particular, we showed that every zig-zag of quasi-isomorphisms and morphisms could be refined to a roof A <- C -> B where C -> A is a quasi-isomorphism. That is, the quasi-isomorphisms of the homotopy category K(A) admits a left calculus of fractions. We also showed that we have a fully faithful functor A -> D(A) identifying A with the complexes X in D(A) such that H^i(X)=0 for all i\neq 0.

    References:

    • Gelfand–Manin, Ch III.2–III.4 (and III.5.2)
    • Huybrechts, Ch 2, 2.1–2.33

  • Fäll ihop Expandera

    Lecture 6 (Feb 26): Calculating using injectives

    We showed that bounded below complexes have injective resolutions (if there are enough injectives). We also showed that K^+(I) -> D^+(A) is an equivalence. More precisely, if I is a bounded below injective complex, then morphisms A -> I in the derived category, i.e. roofs, are the same thing as morphisms A -> I in the homotopy category, i.e., morphisms of complexes up to homotopy.

    References:

    • Huybrechts 2.29–2.40, 2.44
    • Gelfand–Manin III 5.20–25, III 6.1–2
  • Fäll ihop Expandera

    Lecture 7 (Mar 5): Derived functors

    We showed that the right-derived functor RF\colon D^+(\mathcal{A})\to D^+(\mathcal{B}) to an additive functor F\colon\mathcal{A}\to\mathcal{B} exists if \mathcal{A} has enough injectives. Examples: RHom(M,-) , M\overset{L}{\otimes} - , R\mathcal{H}om(M,-) . We also did "complex Hom", Hom^\bullet(A^\bullet,B^\bullet) and its right-derived functors.